pyvista.SolidSphereGeneric

SolidSphereGeneric(radius=None, theta=None, phi=None, center=(0.0, 0.0, 0.0), direction=(0.0, 0.0, 1.0), radians=False, tol_radius=1e-08, tol_angle=None)

柔軟なサンプリングでソリッドな球体を作ります．

2Dの表面である pyvista.Sphere() と比較して，ソリッドな球体は3Dの空間を埋めます．

pyvista.SolidSphere() では線形サンプリングしかできませんが，この関数では各球座標をユーザ定義でサンプリングすることができます． 角度はデフォルトで度単位で指定されます．

PyVistaでは， theta が方位角(地球上の経度のようなもの)を表し， phi が極角(地球上の緯度のようなもの)を表すという慣例を使っています．地球上の緯度とは対照的に，ここでは phi は北極で0度，南極で180度です．デフォルトでは phi=0 が正のZ軸になります．また， theta=0 はデフォルトで正のX軸上にあります．

パラメータ:

radiussequence[float], optional

放射状の点を指定する単調に増加する値のシーケンス．少なくとも2つの点を持ち，非負でなければなりません．

thetasequence[float], optional

単調に増加する一連の値で， theta 点を指定する．少なくとも2つの点を持たなければなりません．範囲が360度以内であればどのような値でもよいです．この値が大きいと，端点の重なり検出で問題が発生する可能性があります．

phisequence[float], optional

単調に増加する一連の値で， phi ポイントを指定します．少なくとも2つの点を持たなければなりません． 0度から180度の間でなければなりません．

centersequence[float], default: (0.0, 0.0, 0.0)

[x, y, z] の中心座標ベクトル．

directionsequence[float], default: (0.0, 0.0, 1.0)

中心 から緯度 phi 度の球の北極を指す [x, y, z] の方向座標ベクトル．

radiansbool, default: False

theta と phi にラジアンを使うかどうか．デフォルトは度です．

tol_radiusfloat, default: 1.0e-8

radius に対する終点検出の絶対許容誤差．

tol_anglefloat, optional

phi``と``θ``の端点検出の絶対許容誤差，単位は radians パラメータの選択によって決定されます．デフォルトは1.0e-8度，または1.0e-8度をラジアンに変換した値です．

戻り値:

pyvista.UnstructuredGrid

ソリッド球体メッシュ．

参考

pyvista.SolidSphere

線形サンプリングによる球体の作成

pyvista.Sphere

外側の2次元表面を表す球体．

例

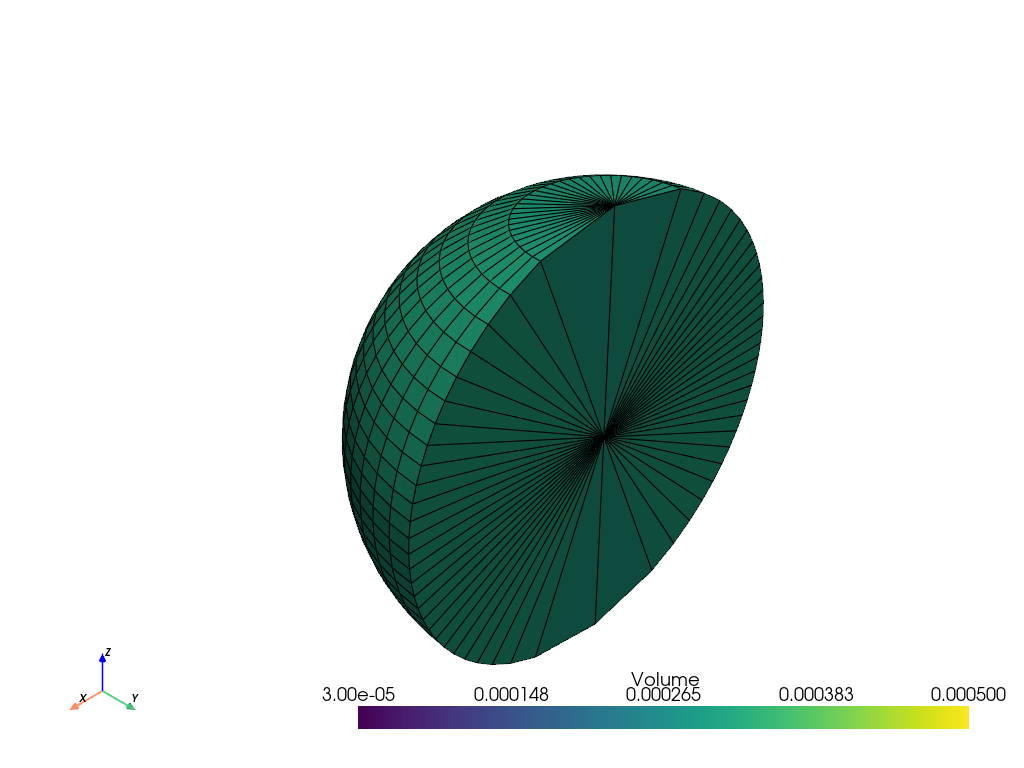
球座標を線形的にサンプリングしても、各半径位置ですべて同じ大きさのセルにはなりません．極に近いセルはより小さなサイズになります．

>>> import pyvista as pv
>>> import numpy as np
>>> solid_sphere = pv.SolidSphereGeneric(
...     radius=np.linspace(0, 0.5, 2),
...     theta=np.linspace(180, 360, 30),
...     phi=np.linspace(0, 180, 30),
... )
>>> solid_sphere = solid_sphere.compute_cell_sizes()
>>> solid_sphere.plot(
...     scalars="Volume", show_edges=True, clim=[3e-5, 5e-4]
... )

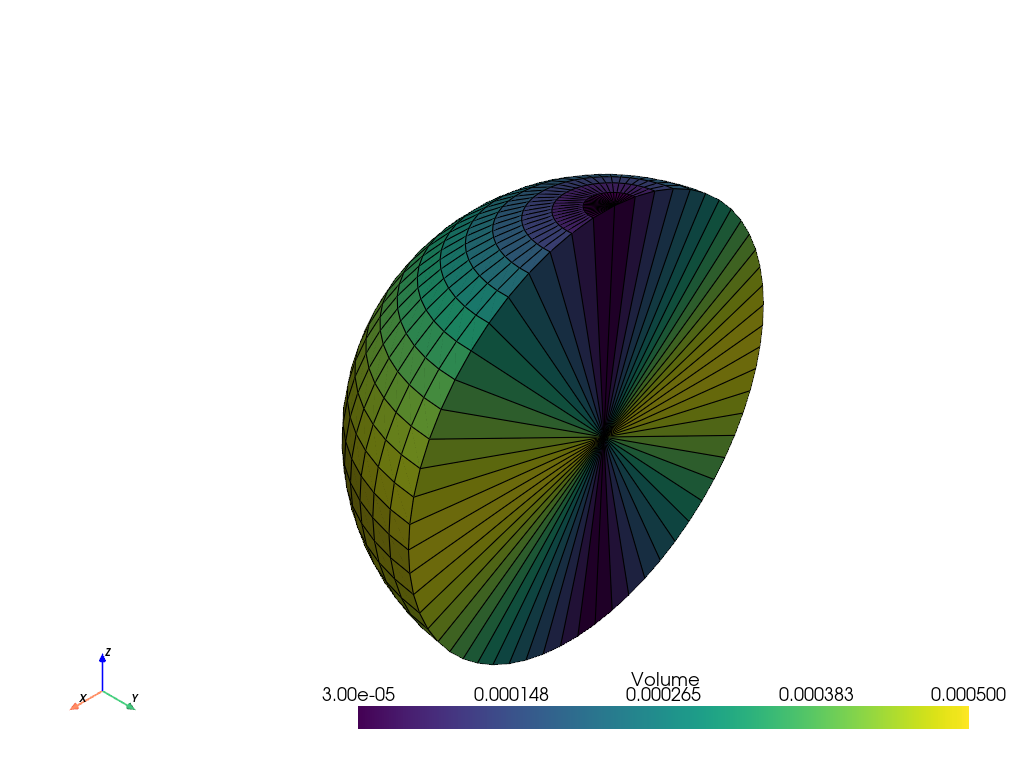
極角を非線形にサンプリングすることで，一貫したセルの体積を得ることができます． Sphere Point Picking を参照してください．

>>> phi = np.rad2deg(np.arccos(np.linspace(1, -1, 30)))
>>> solid_sphere = pv.SolidSphereGeneric(
...     radius=np.linspace(0, 0.5, 2),
...     theta=np.linspace(180, 360, 30),
...     phi=phi,
... )
>>> solid_sphere = solid_sphere.compute_cell_sizes()
>>> solid_sphere.plot(
...     scalars="Volume", show_edges=True, clim=[3e-5, 5e-4]
... )