pyvista.Icosphere

Icosphere(radius=1.0, center=(0.0, 0.0, 0.0), nsub=3)

ICO球を作成します．

ICO球は geodesic polyhedron であり，三角形からなる凸多面体です．

測地線多面体は，より単純な多面体の面を細分化し，新しい頂点を球の表面に投影することで構成されます．測地線多面体は，球に近い直線的な辺と平らな面を持ちます．

パラメータ:

radiusfloat, default: 1.0

ICO球の半径．

centersequence[float], default: (0.0, 0.0, 0.0)

ICO球の中心 ．

nsubint, default: 3

これは，元の pyvista.Icosahedron() の各三角形を細分化した回数です．

戻り値:

pyvista.PolyData

ICO球のメッシュです．

参考

pyvista.Sphere

例

ICO球を作成し，エッジでプロットします．

>>> import pyvista as pv
>>> icosphere = pv.Icosphere()
>>> icosphere.plot(show_edges=True)

このICO球がどのように作られたかを示します．

>>> import numpy as np
>>> icosahedron = pv.Icosahedron()
>>> icosahedron.clear_data()  # remove extra scalars
>>> icosahedron_sub = icosahedron.subdivide(nsub=3)
>>> pl = pv.Plotter(shape=(1, 3))
>>> _ = pl.add_mesh(icosahedron, show_edges=True)
>>> pl.subplot(0, 1)
>>> _ = pl.add_mesh(icosahedron_sub, show_edges=True)
>>> pl.subplot(0, 2)
>>> _ = pl.add_mesh(icosphere, show_edges=True)
>>> pl.show()

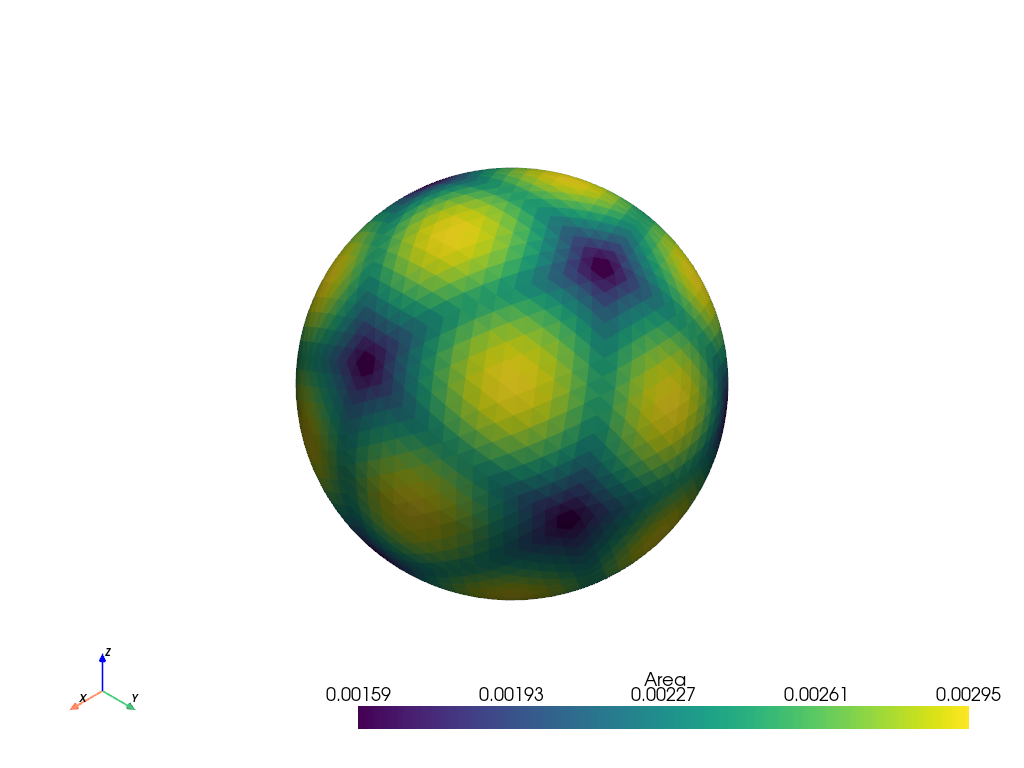
三角形の面積が均一でないことを示します．これは，元の三角形の端から遠いものは，球体への移動距離が長いからです．

>>> icosphere = pv.Icosphere(nsub=4)
>>> icosphere.compute_cell_sizes().plot(scalars='Area')