ブール演算

閉じた（多様な）曲面でブーリアン演算を行う．

ブール/位相演算(交差，結合，切断)法は， pyvista.PolyData メッシュタイプに対してのみ実装され，任意の pyvista.PolyData メッシュから直接アクセス可能である． pyvista.PolyDataFilters をチェックして，次のフィルタを確認してください．

• pyvista.PolyDataFilters.boolean_difference()

• pyvista.PolyDataFilters.boolean_union()

• pyvista.PolyDataFilters.boolean_intersection()

基本的に，ブーリアン結合，切断，交差はすべて同じ操作です．ただ，オブジェクトの異なる部分が最終的に保持されるだけです．

演算子 - は，PyVistaの任意の2つの pyvista.PolyData メッシュの間で使用することができ，最初のメッシュを2番目のメッシュでカットします． これらのメッシュはすべて3角形のメッシュでなければなりません．これは pyvista.PolyData.is_all_triangles で確認できます．

注釈

マージでは， + 演算子をPyVistaの任意の2つのメッシュ間で使用できます．この演算子は，任意の2つのメッシュを結合するために .merge() フィルタを呼び出すだけです．これは boolean_union とは異なり，結果に対して追加の計算を行うことなく，単純に2つのメッシュを重ね合わせるものです．

警告

ブーリアン演算が思った通りに反応しない(例えば，間違った部分が消えてしまう)場合，メッシュの1つが法線を内側に向けている可能性があります．法線を可視化するには， pyvista.PolyDataFilters.plot_normals() を使用してください．

import pyvista as pv

sphere_a = pv.Sphere()
sphere_b = pv.Sphere(center=(0.5, 0, 0))

ブール演算和

pyvista.PolyDataFilters.boolean_union() フィルタを使用して， A と B のブール結合を行います．

2つの多様体メッシュ　A と B の結合は， A にあるメッシュ， B にあるメッシュ，または A と B の両方にあるメッシュとなります．

論理和にはオペランドの順序は関係ありません（演算は可換です）．

result = sphere_a.boolean_union(sphere_b)
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()

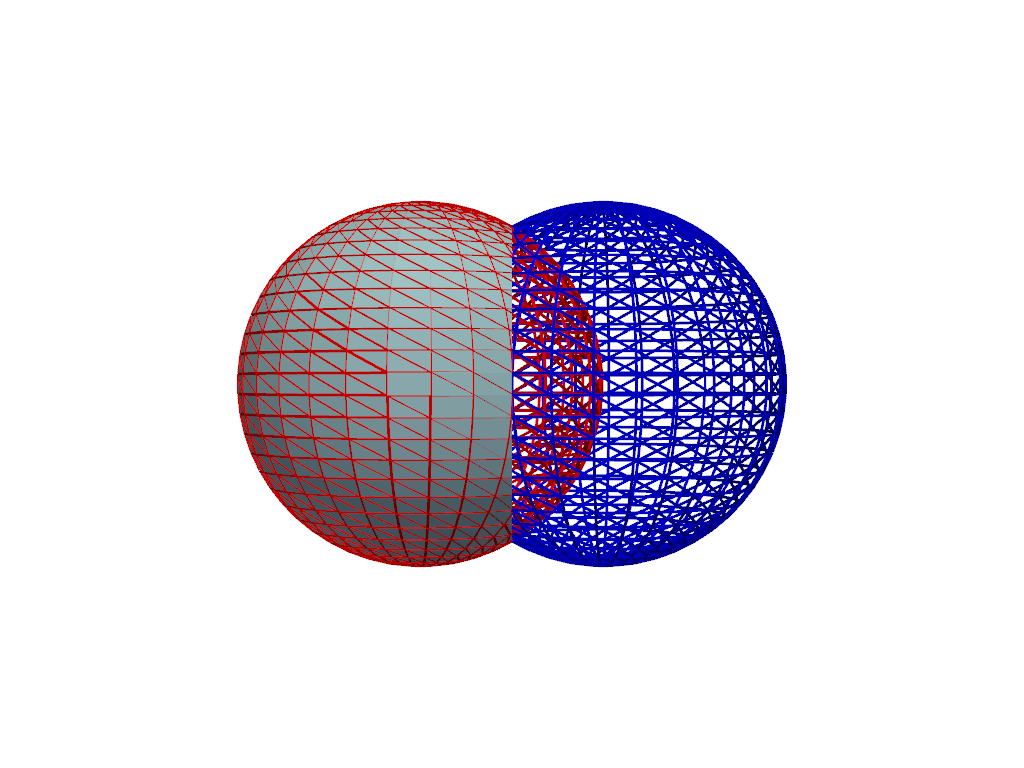
論理差

両方のメッシュが pyvista.PolyData であるため， pyvista.PolyDataFilters.boolean_difference() フィルタまたは - 演算子を使用して A と B のブーリアン値の差を実行します．

2つのマニフォールドメッシュ A と B の差は， A のメッシュのうち B に属さない部分の体積である．

真偽判定にはオペランドの順序が重要です．

result = sphere_a.boolean_difference(sphere_b)
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()

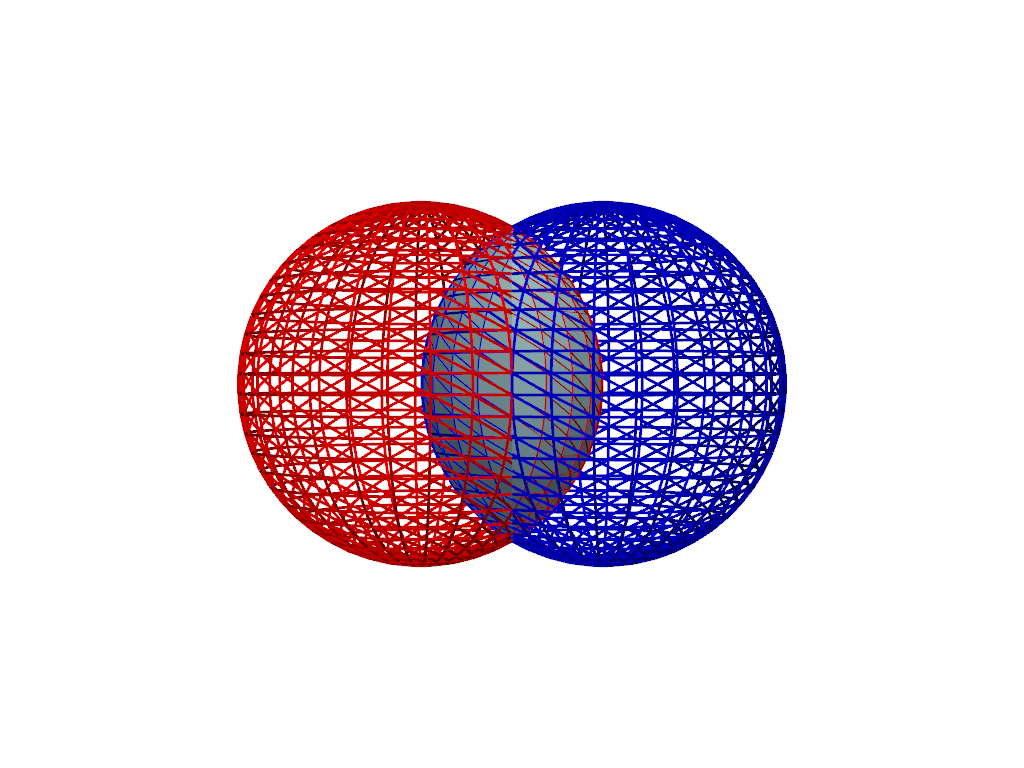
ブール交差

pyvista.PolyDataFilters.boolean_intersection() フィルタを使用して， A と B のブール交差を行います．

2つの多様体メッシュ A と B の交点は， A の体積が B の中にもあるメッシュである．

論理交差にはオペランドの順序は関係ありません（演算は可換です）．

result = sphere_a.boolean_intersection(sphere_b)
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()

法線の反転による挙動

これらのブーリアンフィルターは，法線の向きによって動作が異なることに注意してください．

立方体と球体の両方の法線が外側に向いている状態でのブール型の差分です． これが "normal" の動作です．

cube = pv.Cube().triangulate().subdivide(3)
sphere = pv.Sphere(radius=0.6)
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

立方体の法線を外側に，球体を内側にしたブール値の差．

cube = pv.Cube().triangulate().subdivide(3)
sphere = pv.Sphere(radius=0.6)
sphere.flip_normals()
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

立方体の法線を内側に，球体を外側にしたブール差です．

cube = pv.Cube().triangulate().subdivide(3)
cube.flip_normals()
sphere = pv.Sphere(radius=0.6)
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

立方体と球体の両方の法線を内側にします．

cube = pv.Cube().triangulate().subdivide(3)
cube.flip_normals()
sphere = pv.Sphere(radius=0.6)
sphere.flip_normals()
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')