原子軌道のプロット

水素原子の波動関数(軌道)を可視化します．

インポート

該当するライブラリをインポートします．

注釈

この例は， Matplotlib: 水素波動関数 をモデルにしています．

この例では， sympy が必要です．以下でインストールしてください:

pip install sympy

import numpy as np

import pyvista as pv
from pyvista import examples

データセットの生成

sympy から解析的水素波動関数を評価し，データセットを生成する．

\[\begin{equation} \psi_{n\ell m}(r,\theta,\phi) = \sqrt{ \left(\frac{2}{na_0}\right)^3\, \frac{(n-\ell-1)!}{2n[(n+\ell)!]} } e^{-r / na_0} \left(\frac{2r}{na_0}\right)^\ell L_{n-\ell-1}^{2\ell+1} \cdot Y_\ell^m(\theta, \phi) \end{equation}\]

詳しくは Hydrogen atom をご覧ください．

このデータセットでは，この関数を水素軌道 \(3d_{xy}\) に対して，以下の量子数で評価します．

• 主量子数: n=3

• 方位角量子数: l=2

• 磁気量子数: m=-2

grid = examples.load_hydrogen_orbital(3, 2, -2)
grid

Header	Data Arrays
ImageData Information N Cells 970299 N Points 1000000 X Bounds -2.350e+01, 2.350e+01 Y Bounds -2.350e+01, 2.350e+01 Z Bounds -2.350e+01, 2.350e+01 Dimensions 100, 100, 100 Spacing 4.747e-01, 4.747e-01, 4.747e-01 N Arrays 2	Name Field Type N Comp Min Max real_wf Points float64 1 -1.689e-02 1.689e-02 wf Points complex128 1 -1.689e-02+1.353e-03j 1.689e-02+1.353e-03j

軌道をプロットする

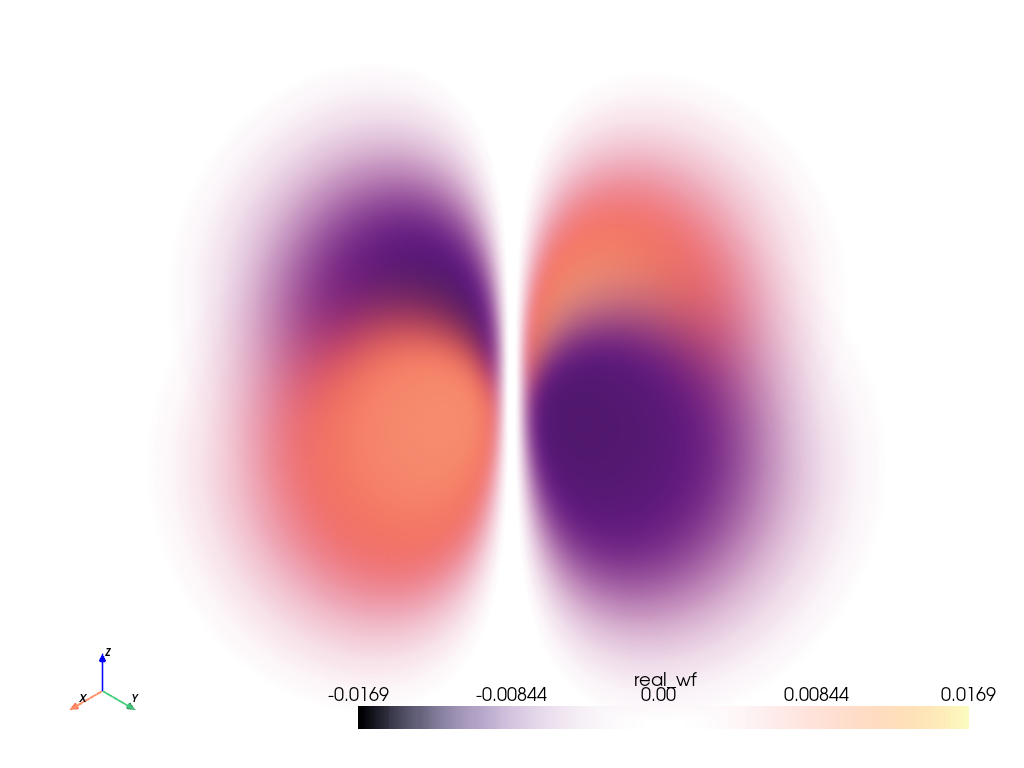
add_volume() を使用して， grid ， real_wf に含まれるデフォルトのスカラーを使用して軌道をプロットしてください．この方法では，電子の確率だけでなく，電子の波動関数の位相もプロットすることができます．

注釈

この軌道の評価波動関数の実数値は [-<value>, <value>] の間で変化するため，デフォルトの不透明度 opacity='linear' を使用することはできません．代わりに，スカラーの絶対値に比例するように不透明度を設定したいので， [1, 0, 1] を使用します．

pl = pv.Plotter()
vol = pl.add_volume(grid, cmap='magma', opacity=[1, 0, 1])
vol.prop.interpolation_type = 'linear'
pl.camera.zoom(2)
pl.show_axes()
pl.show()

軌道の輪郭を等値面としてプロットする

軌道の最大値の10％に等しいときを決定することによって，軌道の輪郭プロットを生成します．これは，この軌道の電子の最も可能性の高い位置を効果的に捉えます．

contour() を評価する際に，スカラーの絶対値を使用して，正相と負相が eval_at を交差する場所を捕捉していることに注目してください．

eval_at = grid['real_wf'].max() * 0.1
contours = grid.contour(
    [eval_at],
    scalars=np.abs(grid['real_wf']),
    method='marching_cubes',
)
contours = contours.interpolate(grid)
contours.plot(
    smooth_shading=True,
    show_scalar_bar=False,
)

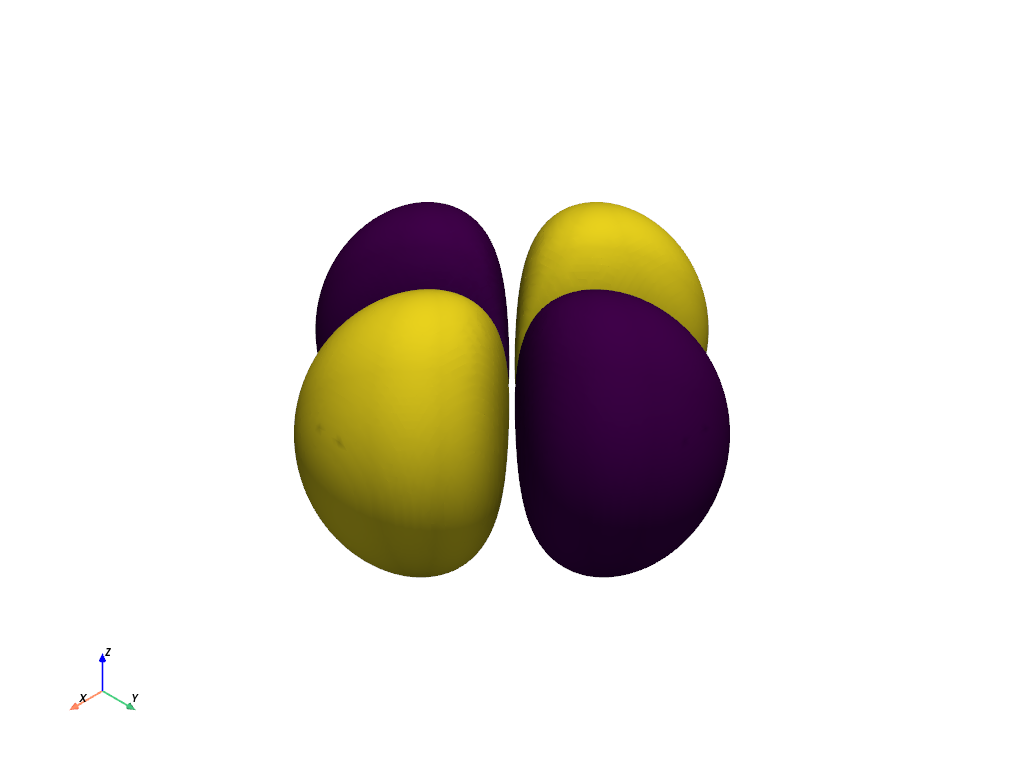
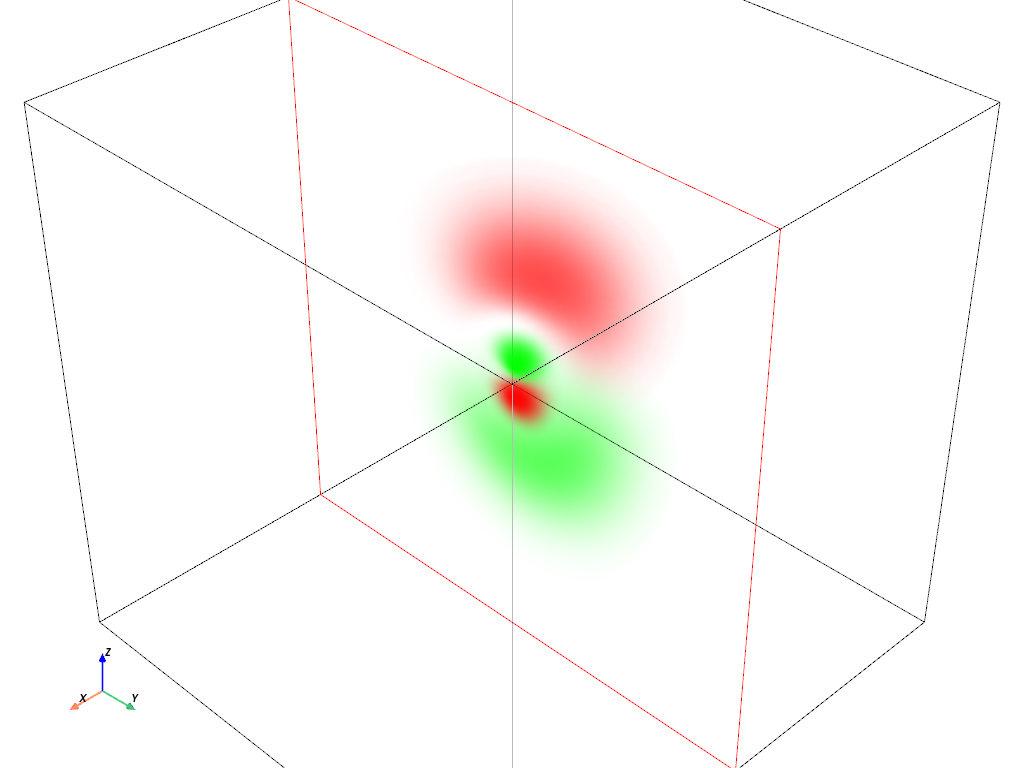
体積プロット: RGBAを使った軌道のプロット

ここで，上の2つのプロットの良いところをいくつか組み合わせてみましょう．体積プロットは "電子雲" 軌道の確率を示すのに最適ですが，カラーマップは等値面プロットほどには現実にマッチしていないようです．

この例では，軌道がプロットされる方法を厳密に制御するために，RGBAカラーマップを使用するつもりです．このために，不透明度は電子がグリッド内のある場所に存在する確率にマッピングされます．これは軌道の波動関数の絶対値の二乗を取ることで実現できます．軌道の色は位相に基づいて設定することができ，単純に orbital['real_wf'] < 0 で得ることができます．

まずは簡単なものから， \(3p_z\) 軌道を考えてみましょう．

def plot_orbital(orbital, cpos='iso', clip_plane='x'):
    """Plot an electron orbital using an RGBA colormap."""
    neg_mask = orbital['real_wf'] < 0
    rgba = np.zeros((orbital.n_points, 4), np.uint8)
    rgba[neg_mask, 0] = 255
    rgba[~neg_mask, 1] = 255

    # normalize opacity
    opac = np.abs(orbital['real_wf']) ** 2
    opac /= opac.max()
    rgba[:, -1] = opac * 255

    orbital['plot_scalars'] = rgba

    pl = pv.Plotter()
    vol = pl.add_volume(
        orbital,
        scalars='plot_scalars',
    )
    vol.prop.interpolation_type = 'linear'
    if clip_plane:
        pl.add_volume_clip_plane(
            vol,
            normal=clip_plane,
            normal_rotation=False,
        )
    pl.camera_position = cpos
    pl.camera.zoom(1.5)
    pl.show_axes()
    return pl.show()


hydro_orbital = examples.load_hydrogen_orbital(3, 1, 0)
plot_orbital(hydro_orbital, clip_plane='-x')

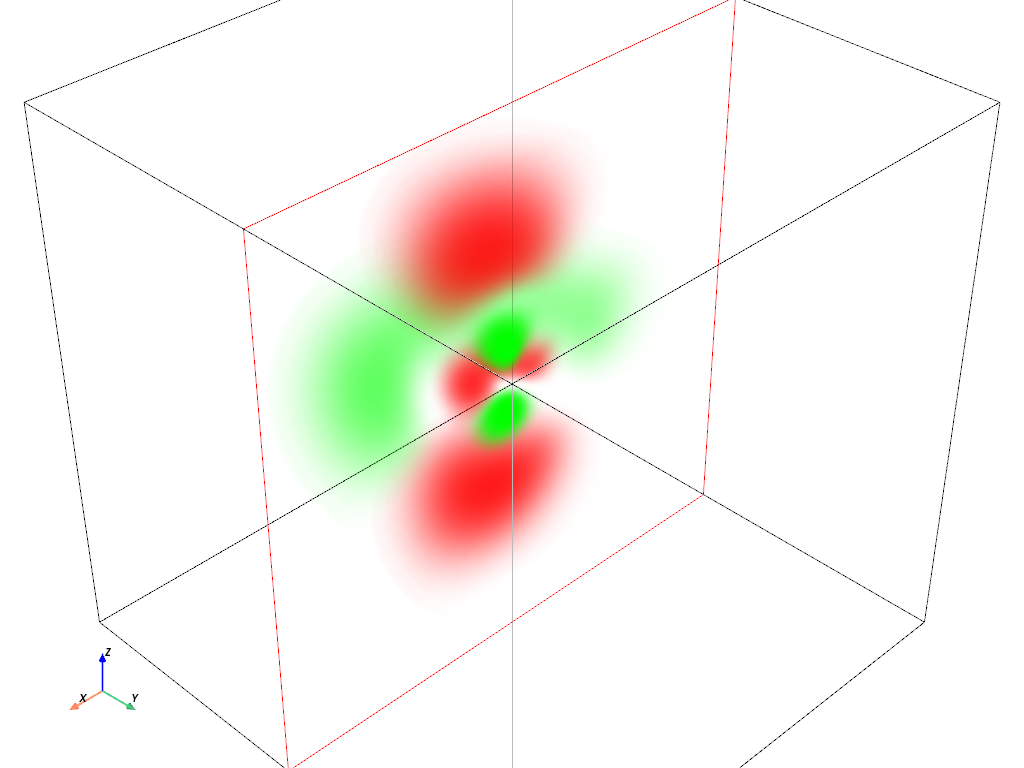
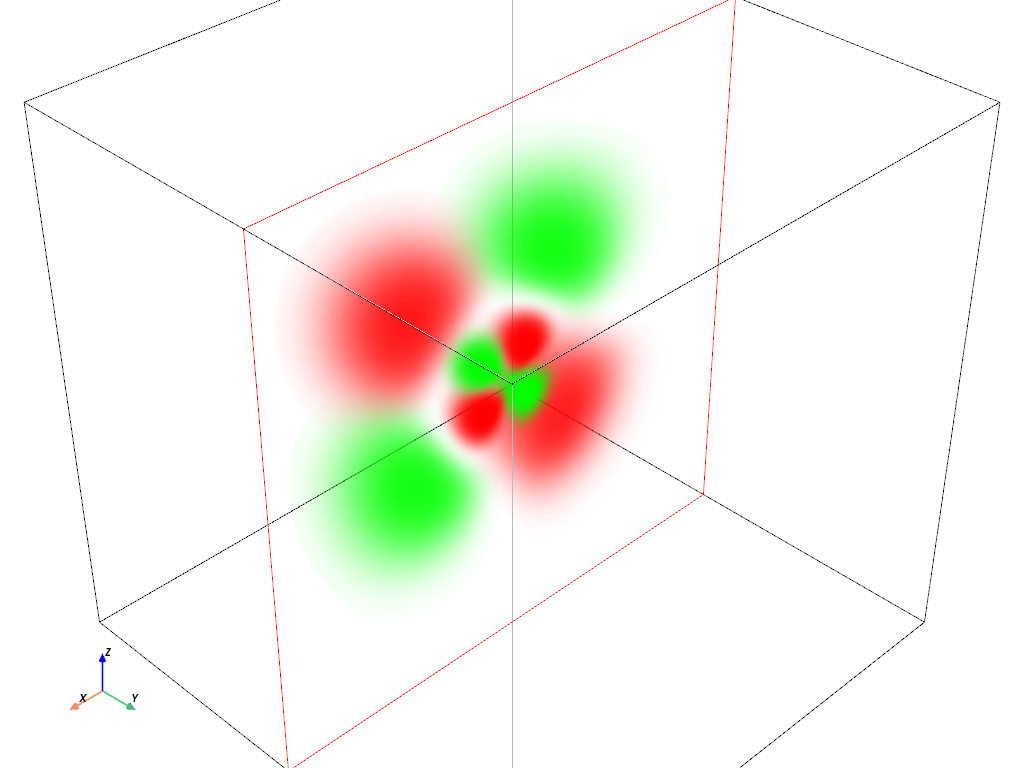
体積プロット: \(4d_{z^2}\) 軌道

hydro_orbital = examples.load_hydrogen_orbital(4, 2, 0)
plot_orbital(hydro_orbital, clip_plane='-y')

体積プロット: \(4d_{xz}\) 軌道

hydro_orbital = examples.load_hydrogen_orbital(4, 2, -1)
plot_orbital(hydro_orbital, clip_plane='-y')

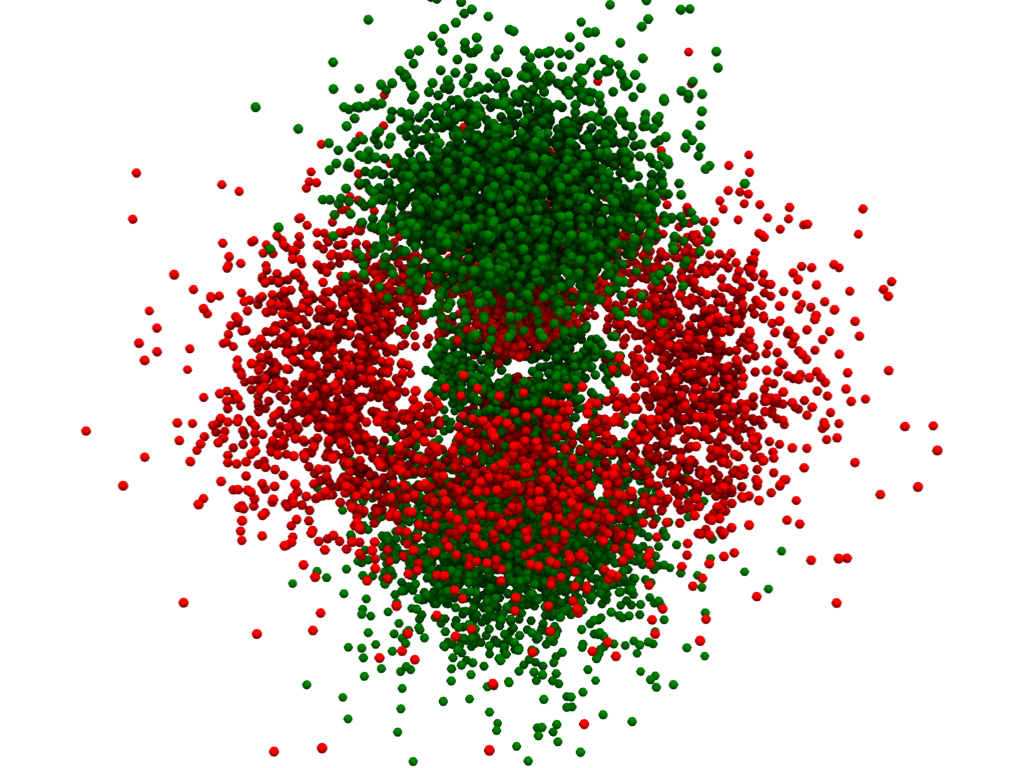
密度プロットによる軌道のプロット

また，3次元密度プロットを用いて原子軌道をプロットすることもできます．そのためには， numpy.random.choice() を使って，電子がその座標にある確率に基づいて pyvista.ImageData のすべての点をサンプリングします．

# Generate the orbital and sample based on the square of the probability of an
# electron being within a particular volume of space.
hydro_orbital = examples.load_hydrogen_orbital(4, 2, 0, zoom_fac=0.5)
prob = np.abs(hydro_orbital['real_wf']) ** 2
prob /= prob.sum()
indices = np.random.choice(hydro_orbital.n_points, 10000, p=prob)

# add a small amount of noise to these coordinates to remove the "grid like"
# structure present in the underlying ImageData
points = hydro_orbital.points[indices]
points += np.random.random(points.shape) - 0.5

# Create a point cloud and add the phase as the active scalars
point_cloud = pv.PolyData(points)
point_cloud['phase'] = hydro_orbital['real_wf'][indices] < 0

# Turn the point cloud into individual spheres. We do this so we can improve
# the plot by enabling surface space ambient occlusion (SSAO)
dplot = point_cloud.glyph(
    geom=pv.Sphere(theta_resolution=8, phi_resolution=8), scale=False, orient=False
)

# be sure to enable SSAO here. This makes the "points" that are deeper within
# the density plot darker.
pl = pv.Plotter()
pl.add_mesh(
    dplot,
    smooth_shading=True,
    show_scalar_bar=False,
    cmap=['red', 'green'],
    ambient=0.2,
)
pl.enable_ssao(radius=10)
pl.enable_anti_aliasing()
pl.camera.zoom(2)
pl.background_color = 'w'
pl.show()

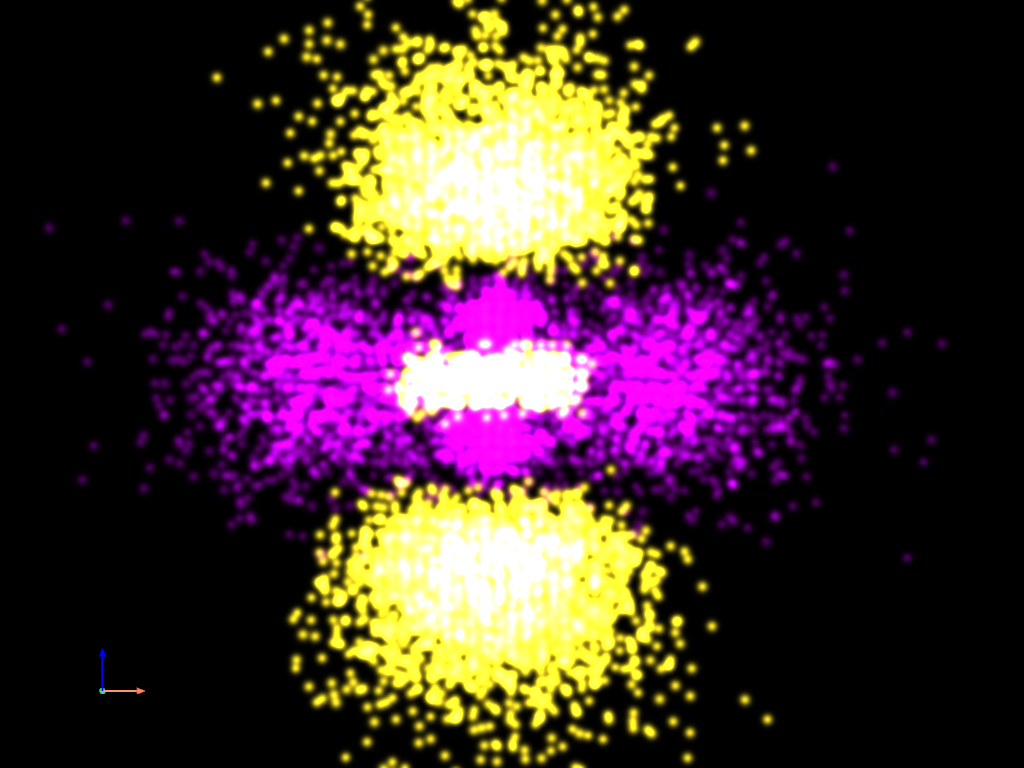
密度プロット - ガウスポイント表現

最後に，同じデータを "ガウスポイント" 表現でプロットしてみましょう．

point_cloud.plot(
    style='points_gaussian',
    render_points_as_spheres=False,
    point_size=3,
    emissive=True,
    background='k',
    show_scalar_bar=False,
    cpos='xz',
    zoom=2,
)