Hertの接触応力を可視化する

次の例は，PyVistaを使って円柱と平板のHertzの接触応力を可視化する方法を示したものである．

この例では，データセットをロードし，円筒とブロックの接触点を表す線を作成し，その線に沿って応力をサンプリングしています．最後に，データセットと応力分布をプロットしています．

背景 Hertzの接触応力とは，接触している2つの曲面の間に発生する応力を指します．1800年代後半にこの現象を初めて記述したドイツの物理学者，Heinrich Rudolf Hertzにちなんで命名されました．Hertzの接触応力は，材料科学や工学など，応力下での材料の挙動が重要視される分野で重要な概念です．

import matplotlib.pyplot as plt
import numpy as np

import pyvista as pv
from pyvista import examples

データセットを読み込む

まず， pyvista.examples モジュールを使ってデータセットを読み込みます．このモジュールでは，応力解析に有用なFEA（有限要素解析）データセットを含む様々なデータセットにアクセスすることができます．

mesh = examples.download_fea_hertzian_contact_cylinder()
mesh

Header

Data Arrays

UnstructuredGrid Information N Cells 132258 N Points 34185 X Bounds -0.000e+00, 2.000e-01 Y Bounds 0.000e+00, 2.500e-02 Z Bounds 0.000e+00, 3.000e-01 N Arrays 16

Name Field Type N Comp Min Max Displacement Points float64 3 -5.000e-04 2.945e-05 vonMises Points float64 1 1.316e+02 1.707e+09 Stress Points float64 6 -3.055e+09 5.274e+08 Strain Points float64 6 -1.937e-02 1.894e-02 PrincipalStress 1 Points float64 1 -1.787e+09 2.586e+08 PrincipalStress 2 Points float64 1 -2.594e+09 3.531e+07 PrincipalStress 3 Points float64 1 -3.078e+09 1.995e+06 PrincipalStrain 1 Points float64 1 -6.976e-04 1.448e-02 PrincipalStrain 2 Points float64 1 -1.145e-02 8.690e-04 PrincipalStrain 3 Points float64 1 -2.787e-02 -8.375e-10 StrainEnergyDensity Points float64 1 1.172e-07 2.307e+07 PlasticStrain Points float64 6 0.000e+00 0.000e+00 EquivalentPlasticStrain Points float64 1 0.000e+00 0.000e+00 Rank Cells float64 1 0.000e+00 1.500e+01 Material Cells float64 1 0.000e+00 1.000e+00 PartID Cells int32 1 1.000e+00 2.000e+00

データセットのプロット

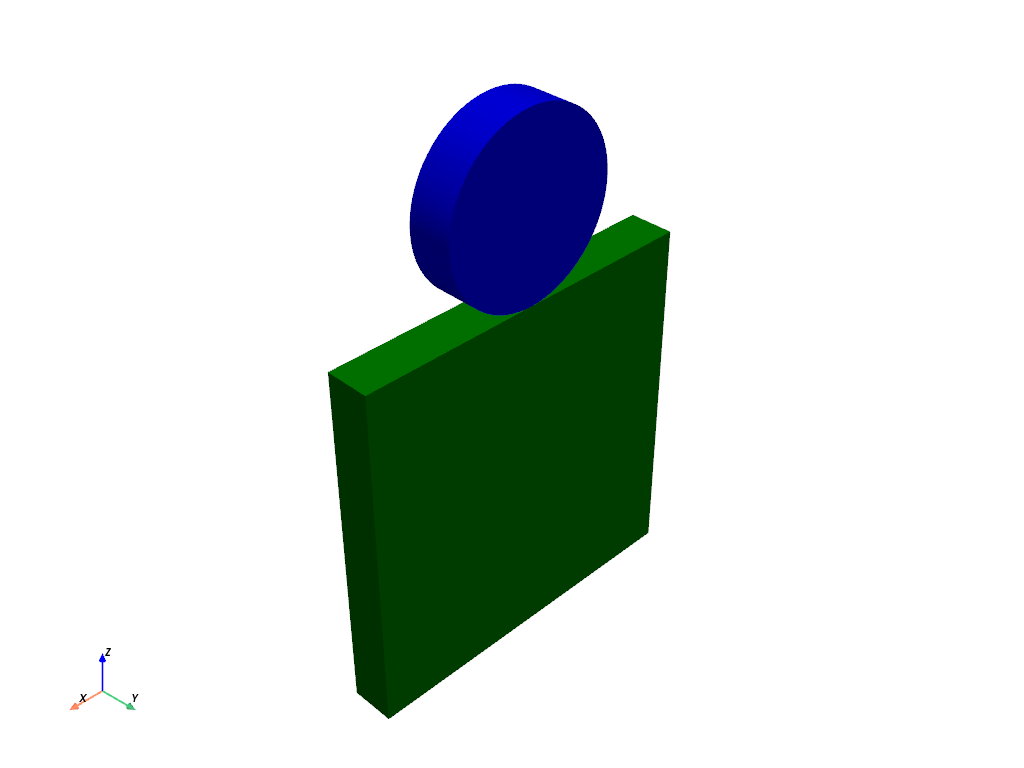
データセットを部分IDごとにプロットする．

mesh.plot(scalars='PartID', cmap=['green', 'blue'], show_scalar_bar=False)

接触点を表す線を作る

円柱とプレートの接触点を表す線を作ります．

ypos = 0.024
a = [0.1, ypos, 0.2 - 1e-4]
b = [0.095, ypos, 0.2 - 1e-4]
line = pv.Line(a, b, resolution=100)
line.clear_data()
line

PolyData	Information
N Cells	1
N Points	101
N Strips	0
X Bounds	9.500e-02, 1.000e-01
Y Bounds	2.400e-02, 2.400e-02
Z Bounds	1.999e-01, 1.999e-01
N Arrays	0

線に沿った応力のサンプリング

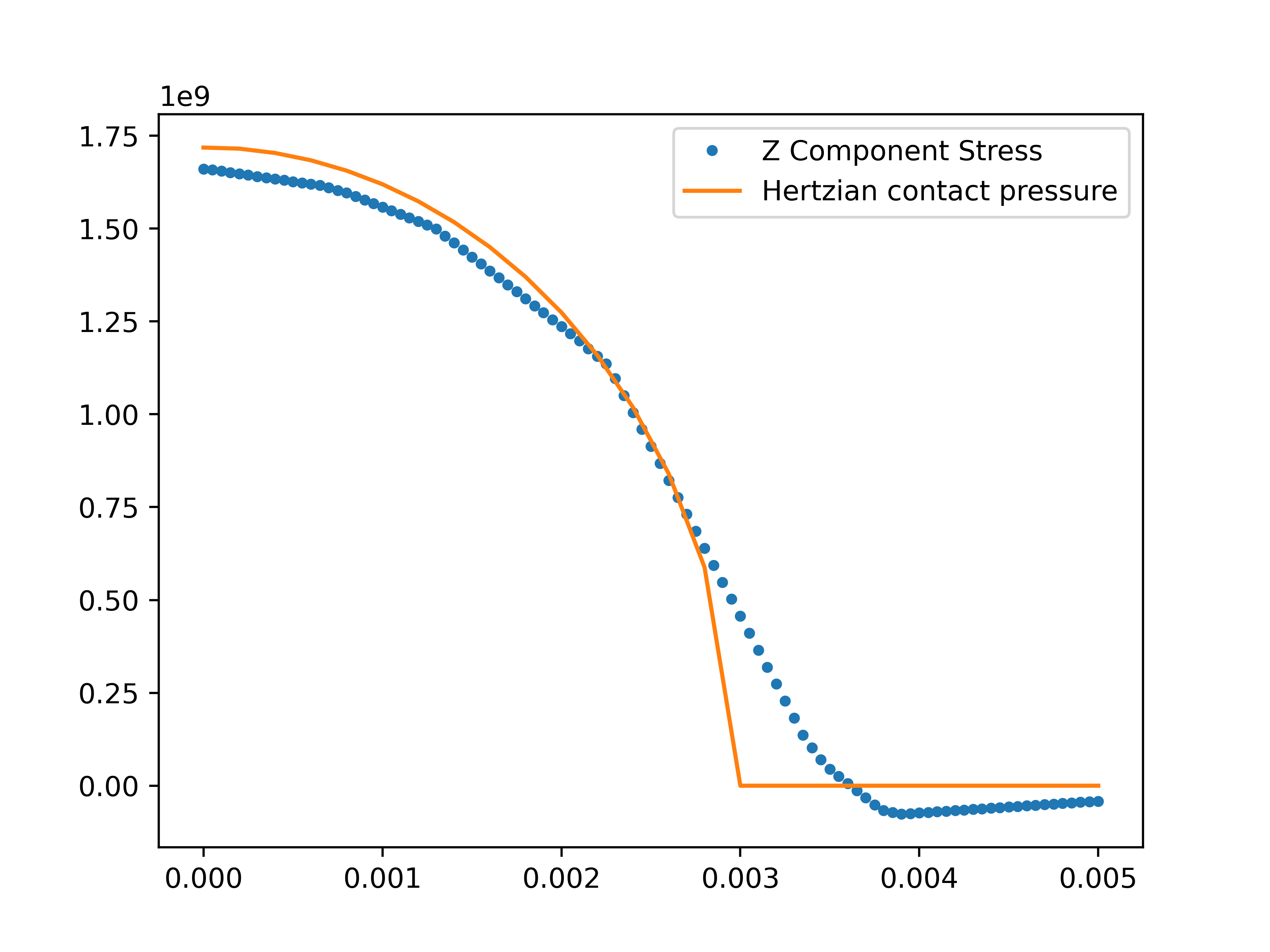
接触端に沿ったZ成分の応力をサンプリングし，予想される圧力と比較することができます．

期待値の配列はHertzの接触圧であり，非粘着性接触問題の解析的解である．これらの値の計算は読者に任された練習です（円柱の半径は0.05です）． Contact Mechanics を参照してください．

# Sample the stress
sampled = line.sample(mesh, tolerance=1e-3)
x_coord = 0.1 - sampled.points[:, 0]
samp_z_stress = -sampled['Stress'][:, 2]

# Expected Hertzian contact pressure
h_pressure = np.array(
    [
        [0.0000, 1718094092],
        [0.0002, 1715185734],
        [0.0004, 1703502649],
        [0.0006, 1683850714],
        [0.0008, 1655946243],
        [0.001, 1619362676],
        [0.0012, 1573494764],
        [0.0014, 1517500856],
        [0.0016, 1450208504],
        [0.0018, 1369953775],
        [0.002, 1274289906],
        [0.0022, 1159408887],
        [0.0024, 1018830677],
        [0.0026, 839747409.8],
        [0.0028, 587969605.2],
        [0.003, 0],
        [0.005, 0],
    ]
)

plt.plot(x_coord, samp_z_stress, '.', label='Z Component Stress')
plt.plot(h_pressure[:, 0], h_pressure[:, 1], label='Hertzian contact pressure')
plt.legend()
plt.show()

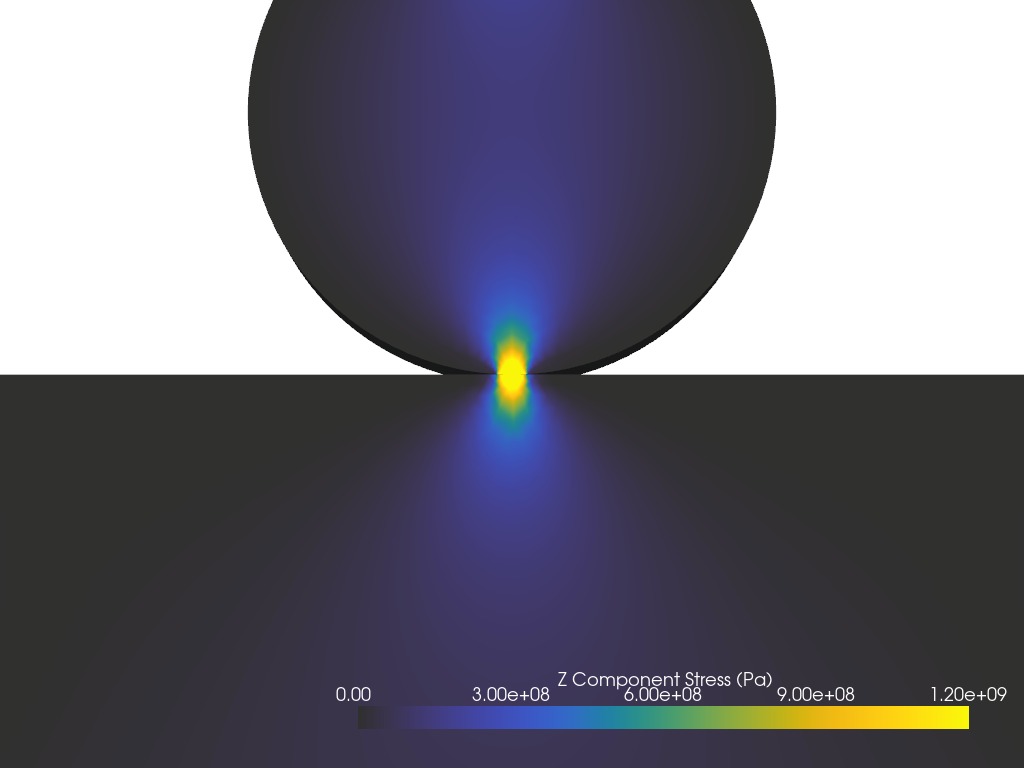
Z応力分布の可視化

これで，Z応力分布を可視化することができます． pyvista.Plotter を使用してプロットウィンドウを作成し，データセットをそこに追加します．

pl = pv.Plotter()
z_stress = np.abs(mesh['Stress'][:, 2])
pl.add_mesh(
    mesh,
    scalars=z_stress,
    clim=[0, 1.2e9],
    cmap='gouldian',
    scalar_bar_args={'title': 'Z Component Stress (Pa)', 'color': 'w'},
    lighting=True,
    show_edges=False,
    ambient=0.2,
)
pl.camera_position = 'xz'
pl.set_focus(a)
pl.camera.zoom(2.5)
pl.show()