多面体による非構造化グリッド

この例では，多面体を使ってシンプルな pyvista.UnstructuredGrid を構築する方法を紹介します．VTKの型を使用して，どのタイプのセルを構築するかを決定します．

まず，必要なライブラリをインポートします．

import pyvista as pv

ポイントの定義

この例では，1つのグリッドに複数のセルを混在させることにします．ここでは，各セルを定義するポイントを作成します．

注釈

各セルが孤立した点の集合を持つ必要はありません．この例では，孤立したセルを作成するために，このような方法をとっています．

quad_points = [
    [0.0, 0.0, 0.0],  # 0
    [0.0, 0.01, 0.0],  # 1
    [0.01, 0.01, 0.0],  # 2
    [0.01, 0.0, 0.0],  # 3
]
polygon_points = [
    [0.02, 0.0, 0.0],  # 4
    [0.02, 0.01, 0.0],  # 5
    [0.03, 0.01, 0.0],  # 6
    [0.035, 0.005, 0.0],  # 7
    [0.03, 0.0, 0.0],  # 8
]
hexa_points = [
    [0.0, 0.0, 0.02],  # 9
    [0.0, 0.01, 0.02],  # 10
    [0.01, 0.01, 0.02],  # 11
    [0.01, 0.0, 0.02],  # 12
    [0.0, 0.0, 0.03],  # 13
    [0.0, 0.01, 0.03],  # 14
    [0.01, 0.01, 0.03],  # 15
    [0.01, 0.0, 0.03],  # 16
]
polyhedron_points = [
    [0.02, 0.0, 0.02],  # 17
    [0.02, 0.01, 0.02],  # 18
    [0.03, 0.01, 0.02],  # 19
    [0.035, 0.005, 0.02],  # 20
    [0.03, 0.0, 0.02],  # 21
    [0.02, 0.0, 0.03],  # 22
    [0.02, 0.01, 0.03],  # 23
    [0.03, 0.01, 0.03],  # 24
    [0.035, 0.005, 0.03],  # 25
    [0.03, 0.0, 0.03],  # 26
]
points = quad_points + polygon_points + hexa_points + polyhedron_points

セルの接続性

接続性は，各セルを構成する点のインデックスを記述します．各セルのコネクティビティの最初の項目は，そのセルが持つ項目の数です．例えば，4角形のセルは点 [0, 1, 2, 3] と合計4つの点から構成されるので， [4, 0, 1, 2, 3] がその接続性を表していることになります．

注釈

この例では簡単のためにリストを使っていますが，内部的にはPyVistaはこれらのリストを dtype=pyvista.ID_TYPE で numpy.ndarray に変換してVTKに渡します．

他のすべてのセルタイプにも同じアプローチが可能です．

quad = [4, 0, 1, 2, 3]
polygon = [5, 4, 5, 6, 7, 8]
hexa = [8, 9, 10, 11, 12, 13, 14, 15, 16]

多面体接続配列

多面体の接続配列は，他のセルタイプとは異なる定義になっています．多面体の場合，次のような形式で面を設定する必要があります．

[NItems, NFaces, Face0NPoints, Face0Point0, Face0Point1..., Face0PointN-1, Face1NPoints, ...]

ここで:

• NItems は，多面体を表現するために必要なリストのアイテムの総数を指します．

• NFaces は，多面体が持つ面の数です．

• Face0NPoints は，最初の面が持つ点の数です．

• Face0Point0...Face0PointN-1 は face0 を記述する各点です．

polyhedron_connectivity では，最初の項目は NFaces です． NItems は polyhedron に追加されます．

polyhedron_connectivity = [
    # NItems will go here
    7,  # number of faces
    5,  # number of points in face0
    17,  # point index 0
    18,  # point index 1
    19,  # point index 2
    20,  # point index 3
    21,  # point index 4
    4,  # number of points in face1
    17,  # point index ...
    18,
    23,
    22,
    4,
    17,
    21,
    26,
    22,
    4,
    21,
    26,
    25,
    20,
    4,
    20,
    25,
    24,
    19,
    4,
    19,
    24,
    23,
    18,
    5,
    22,
    23,
    24,
    25,
    26,
]

# note how we retroactively add NItems
polyhedron = [len(polyhedron_connectivity)] + polyhedron_connectivity

セル配列

ここで， pyvista.UnstructuredGrid の入力セル配列を作成します．ここでは，すべてのセルをフラットリストで結合します．内部的には，先に説明した NItems を使用して，どのノードがどのセルに属しているかを判断します．

cells = quad + polygon + hexa + polyhedron

セルタイプ

セル配列に定義した各セルに対して，セルの種類を指定する必要があります．

このリストの項目数は，接続配列のセル数と一致させる必要があります．

celltypes = [pv.CellType.QUAD, pv.CellType.POLYGON, pv.CellType.HEXAHEDRON, pv.CellType.POLYHEDRON]

グリッドの作成

グリッドの作成には，構築したセル配列，セルの種類，面を記述する点を使用します．

grid = pv.UnstructuredGrid(cells, celltypes, points)

メッシュをプロットする

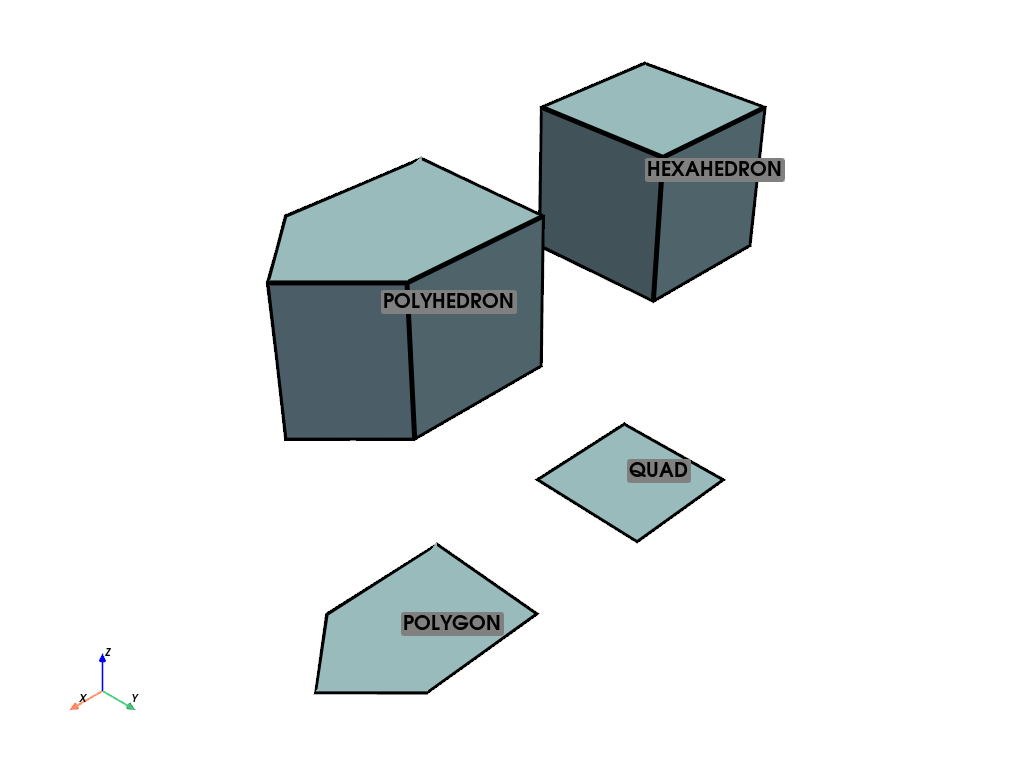
最後に，作成したグリッドをプロットすることができます．わかりやすくするために，各セルの中心にラベルを貼ってください．

pl = pv.Plotter()
pl.show_axes()
pl.add_mesh(grid, show_edges=True, line_width=5)
pl.add_point_labels(
    grid.cell_centers().points,
    ['QUAD', 'POLYGON', 'HEXAHEDRON', 'POLYHEDRON'],
    always_visible=True,
    font_size=20,
)
pl.show()